The World is Sound

The myths from many different cultures have always told us: God created the world from sound – from music. Across the globe there are creation myths which include music as one of the factors playing a major role in the creation of the world. “In the beginning was the Word” according to the Gospel of John. But a spoken word is also a sound. Harmonics (Greek: harmonikos) means “related to music”, but harmonics as a field of studies encompasses far more than the musical “theory of harmony” . In fact, it is the ancient study of the sound of the world.

“In the beginning, God made a clay statue as an image of the Divine and asked the human soul to enter it. The soul refused, regarding this forced incarnation as a kind of imprisonment. The soul was accustomed to fly freely about the celestial realms, unfettered and unbound. So God requested the angels to play their music. The angelic song brought the soul such ecstasy that it willingly entered the body of clay, believing that it would hear the music better in physical form.” “But,” Hafiz continued, “angelic music was more than God’s lure. Many say that on hearing the music, the soul entered the body. But in reality, the soul itself was music.”

(Story attributed to Hafiz, one of the greatest Persian poets.)

The study of harmonics can be traced back to Pythagoras around 600 BC. By experimenting with a one-string musical instrument, the monochord, he discovered that there is a clear connection between numbers and sounds – in other words, between quantitative and qualitative, between string length and pitch and thus also between reason and emotion, between matter and spirit.
The numbers begin to sound and matter becomes animated: Fig. 1

Pythagoras’ new insight into the structure of music became a source of scientific inspiration for the Ancient Greeks and made a lasting impression on their culture. He saw a two-way relationship between pitch and number:

1) Tracing the qualitative back to the quantitative:
Example: “Ah, that has a particular sound because it has a particular proportion.” Explaining a quality was a completely new idea and set a new direction within the world of the Greeks and pre-classical civilizations, which were overflowing with myth and symbolism. This new view of the world went on to become the foundations of modern Occidental science. Nonetheless, Pythagoras was also thinking in the other direction:

2) The assessment of the quantitative (number, all matter) by means of the qualitative was just as important to him.
Example: “The proportion is good if it touches my soul – if it is ‘beautiful’.” This aspect has been increasingly neglected since the end of the Classical Antiquity. Science and technology have distanced themselves from the human soul and taken on a life of their own.

“In the beginning there was darkness. Amaterasu, the goddess of the sun, had not yet been enthroned in heaven. She was living in a cave and the world was cold, inhospitable and lifeless.

So God took six huge bows, tied them together and thus created the first harp, which he used to play wonderful melodies. Attracted by these tunes, the dazzling nymph Ameno-Uzeme appeared. Entranced by the harp’s music, she began to dance – and also to sing. The sun goddess Amaterasu became aware of the distant music and wanted to hear better, so she peeked out of her cave. In that moment, the world was bathed in light. The sun could now be seen and its rays felt – flowers, bushes and trees began to grow. Filled with light, the earth attracted creatures of the air, water and land – and people appeared, too. The gods decided to cultivate song and dance from that moment on, in order to ensure that the sun goddess would never creep back into her cave. They knew:

It was the sun that made life possible, but without the harp’s music and the nymph Ameno-Uzume’s songs, Amaterasu, the sun goddess, would never have taken up her rule on her sky throne. She would have remained in her cave forever. So it was with sound, in the form of music and dance, that the world began.”

(Creation myth from Japan.)

The sun begins to shine because music begins to sound: this is the Japanese legend, And now the recently developed science of sonoluminescence was born with the discovery that sound can lead to the production of light. When a tiny gaseous cavity (bubble) within a liquid is subjected to a high-frequency (30,000 Hz) sound wave of sufficient intensity, it can be induced to collapse over and over again in a periodic fashion, emitting a burst of light each time it collapses and generating temperatures comparable to those at the surface of the sun. In particular circumstances the bubble is held in place and this situation becomes stable.

Who was Pythagoras?
Pythagoras was born in 570 BC on the island of Samos. As the tyrant Polykrates seized power on the island, Pythagoras left and undertook extensive and long journeys. In Egypt he was initiated into the secret knowledge of the priests. This may well be the source of the Pythagorean theorem which bears his name: a2 + b2 = c2. Fussnote 1

At the age of 40, Pythagoras settled in Croton, a Greek colony in southern Italy, and became the main focus of an organisation later known as the Pythagorean school. Pythagoras the scholar attracted influential followers but later the group was nonetheless accused of treachery and became subject to attack. It is said that Pythagoras and 40 of his followers were burnt to death in an attack on a gathering of the Pythagoreans. The power of the organisation was destroyed but we can safely assume that his teachings were passed on in secretive groups for centuries afterwards.

What did Pythagoras teach?
The Pythagorean secret society in Croton was structured along the lines of the Egyptian mystery schools, teaching a carefully guarded “Theology in the form of mathematical figures”. There are no extant texts which are considered authentic original works of Pythagoras himself, but many of his teachings were reproduced by his disciples. Some of these cryptic statements or theories are so beautiful that I would like to quote them here:

1. “The whole world is harmony and number.” (Aristoteles)
2. “The nature of Number and Harmony admits of no Falsehood; for this is unrelated to them.“ (Philolaus)
3. “Harmony is the unification of the diverse and the reconciliation of the contrary-minded. Harmony always arises from opposites.”
4. “The world’s being is the harmonious compound of Unlimited and Limiting principles; such is the totality of the world and all it contains.”
5. “Even above the Limit and Unlimited there is the principle behind these two principles of manifest things – the unmanifest cause of the causes: God.”

How did the Pythagoreans arrive at these statements? And how could they have developed all of these conclusions by considering the laws of music and mathematics?

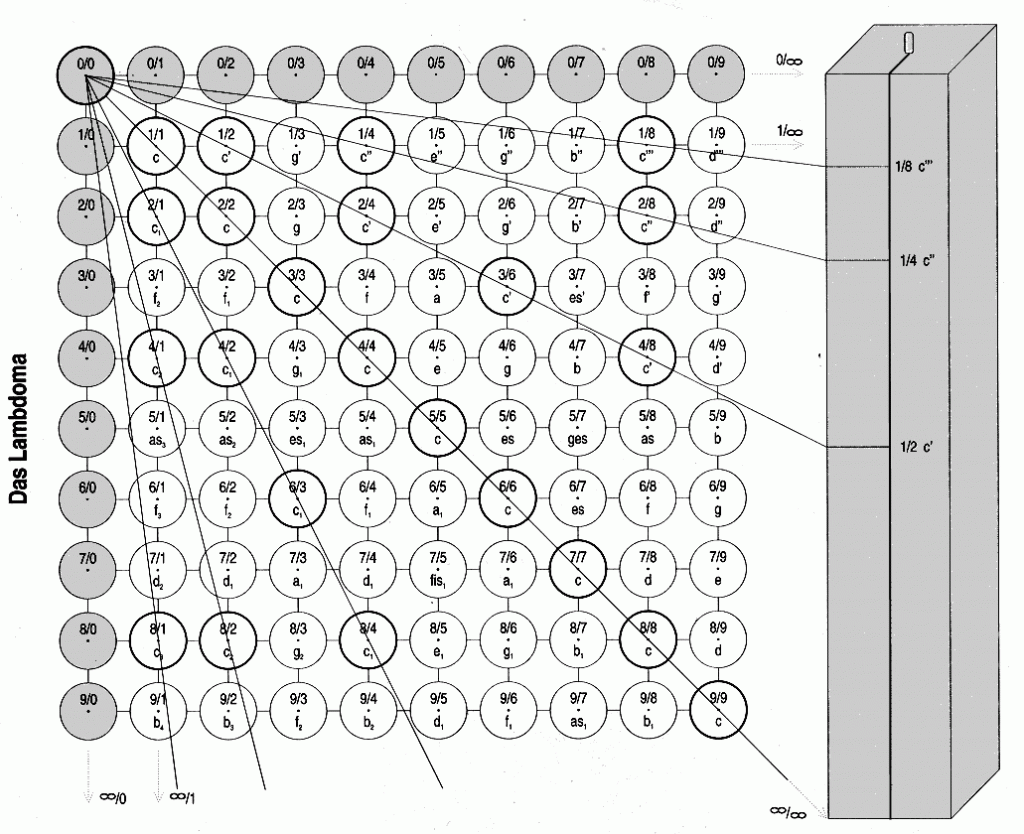
The heart of Pythagorean teachings was the Pythagorean Table, the Lambdoma, which was rediscovered and reconstructed in the mid-19th century by Albert Thimus. In its original form, the diagram was shaped like the Greek letter lambda, which explains its name. It is constructed according to strict mathematical laws: Fig. 2

1. Horizontally, the numerator remains constant and the denominator increases towards infinity. This means that the fraction becomes ever smaller, heading towards a limit value of zero but never reaching zero.
2. Vertically, the denominator remains constant and the numerator increases towards infinity. So the numeric value grows towards infinity.
3. The values along the main diagonal are always 1.
4. The point 0/0 can be deduced by extending the two outer rows or also by logically extending the main diagonal backwards.

We already know that every ratio of whole numbers can be represented as a musical interval. If we set 1/1 as the basic pitch c, then for 1/2 we have c’, for 1/3 g’ and so on. This leads to the following:

1. Horizontally we have a range of harmonic series.
2. Vertically we have series made up of undertones (i.e. the overtone intervals from the harmonic series are reflected downwards). 2:1 means a doubled string length, i.e. the pitch sounds one octave lower, the frequency halves. Undertones have not yet been proven to occur naturally but using mathematics they can be deduced with astonishing regularity.
3. An undertone series forms based on each tone in the harmonic series (overtone series), and an overtone series forms based on each tone in the undertone series.
4. Horizontally, major triads form at the 3rd, 4th and 5th places.
5. Vertically, minor triads form at the 3rd, 4th and 5th places.
6. The fundamental tone c extends along a diagonal through the diagram. All of the tones above this diagonal are higher in pitch than c, those below are lower.
7. All identical tones (fractions with the same value) lie on a straight line.
8. All of these straight lines can be seen to radiate out from a single point, which corresponds to the fraction 0/0.

The same tone values repeat themselves in different environments. The further they are from the source, the more lustrous and diverse their environment.

For the Pythagoreans, this could be seen as evidence of reincarnation. All of the same-tone lines converge at the point 0/0 – at the point which lies behind everything but does not actually materialise itself: the highest principle of Creation – the cause of causes, God (re-ligion = trace back). One could suppose that the same-tone lines converge at the point 1/1, since this was the starting point and fundamental tone for our harmonic series. This is the material, earthly creation point – father and mother. However, they don’t; instead they converge at the non-material 0/0. Mathematically speaking, the fraction 0/0 can be regarded as both “everything” and “nothing”. It contains everything but cannot be expressed in anything. 0/0 cannot be grasped in any accessible terms. For the Pythagoreans, it was a symbol for God. The Kabbalists spoke of “En-Sof” – the Abstract, the Absolute, the Primeval Idea. For the Christian mystic Jakob Böhme it was “that ground from whence all things proceed” and Teilhard de Chardin called it the Omega Point.

There is no God external to ourselves. Neither is it the case that there is no God. 0/0 is contained within everything. In other words, “everything” is a very special case of 0/0. Considered from the other direction, 0/0 only comes into existence because of the material, audible world. Without this, it remains a thought concept. The statements and conclusions which a consideration of Lambdoma can lead to (for music and for vibrations) can be applied to all matter, since one thing that we are now fairly certain of is that matter vibrates. Upon closer examination, all fundamental particles break down into ever smaller particles. At the end we are left with vibration, rhythm, energy. Having reached this limit, even physicists have been known to speak of Love or God.

At the heart of every Piece of matter lies a “base of God”.
This is the inner centre Through which Things strive towards one another.

(Teilhard de Chardin)

From harmonics studies:
Both recent and older studies have shown that the laws of harmonics are visible not only in the fields of music and mathematics, but also in the ratios and proportions of the macrocosmos, the microcosmos and our earthly world. Everywhere we find the prevalence of consonant harmonies – fractions composed of low integers. Here is a selection of these occurrences.

1) Spectral lines
In a spectroscope, light can be broken down into coloured bands clearly separated by black lines. Every chemical element and every star has its own characteristic spectrum, which can be interpreted harmonically.

2) Astronomy
The early Pythagoreans already had the idea of an acousitic “harmony of the spheres”. Aristotle introduced the notion that the planets emitted tones in the heavens due to their orbits and the ratios which could be obtained by comparing their distance and speed. These ratios were musical. Renewed interest in ancient thought during the Renaissance led to a revival of the Pythagorean school’s ideas. Johannes Kepler (1571-1630) had been fascinated from his youth by ideas of the harmony of the world. In his book of that name (“Harmonices Mundi”) he offered the first proofs that planetary orbits exhibited accordance with musical laws. He discovered that the planets go around the sun along elliptical orbits and that their speed at the perihelion (closest to the sun) is higher than at the aphelion (furthest away). Comparing the ratios between these orbital speeds, he found only those corresponding to harmonic intervals. In fact, they are almost exclusively major triad tones! Of course, these tones are not directly audible, but we can set a monochord to produce them.

In 1940, Francis Warrain expanded Kepler’s studies by adding the values for the newly discovered planets Uranus, Neptune and Pluto. He was able to confirm all of Kepler’s values apart from that for Mercury, finding familiar musical intervals for all 39 ratios. If we consider all the intervals as overtones of a common fundament c, then all but 4 of the tones belong to the major scale.

3) Crystals
Crystals arise in accordance with laws of symmetry, so they have very simple orders which can be interpreted harmonically. These properties are already expressed in the atomic structure of the crystal. There are 32 crystal classes, covering all existing specimens. Crystal symmetry is classed in terms of rotation and mirroring. For rotational symmetry, the only possible values are 360’, 180’, 120’, 90′ and 60′, which corresponds to the fractional series 1/1, 1/2, 1/3, 1/4, 1/6 (where 1/1 = 360′), and can in turn be interpreted harmonically (c, c’, g’, c”, g”).

At the beginning of the 20th century, the German mineralogist Victor Goldschmidt discovered a mathematical formula to classify how crystals form surfaces. His table corresponds exactly to the Pythagorean Lambdoma right up to the number 4 (or 1/4) – this is particularly interesting because he was not familiar with the Lambdoma.

4) Chemistry
The three most important chemical elements for organic life – hydrogen, carbon and oxygen – have a remarkable harmonic relationship to each other if we consider their nuclear charge and atomic weight. If these numbers are taken as the partials of a harmonic series, this produces two number series comprising the same tone values but from different octaves. And they exhibit the most consonant of all the basic intervals: octaves and perfect fifths. When atoms bond with each other and form molecules, they do so with the greatest possible symmetry and very often this results in the shapes known as the “5 Platonic Solids”. These solids were first described by Plato in his dialogue “Timaeus”. Each of them is formed by fitting together identical regular polygons and there are no other possible solids that can be formed in a similar way. When the numbers of edges and surfaces for each solid are expressed as a ratio, they can be said to produce sounds that are predominantly in the major triad.

The five Platonic solids

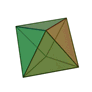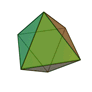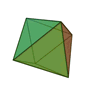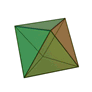
From left to right: Icosahedron, Octahedron, Tetraeder, Hexahedron, Dodecahedron

5. Botany
As a morphological constant, the number 5 is missing in the structure of crystals. It first appears in this role when we look at the plant world. For example, there are plants with five petals or stamens. The number five corresponds to a third in the harmonic series, often known as the “gender tone” in music theory because it determines the tonality (the “tone gender”). (major c-e-g = major third; minor c-e flat-g = minor third) Fussnote 2. Goethe discovered that expressing the intervals of the musical scale as angles could lead to a diagram resembling the form of his “Primal Leaf” Fig. 3 – In other words, the musical scale contains the leaf form within it.

The universe and I exist together, and all things and I are one.
Since all things are one,
What need is there for speech?
But since I have already said,
That all things are one, how can speech be not important?
…
Behind the divisible there is always something indivisible,
Behind the disputable there is always something indisputable.
You ask: What?
The wise man carries it in his heart.

(Zhuangzi)

6) The Art of Building – Architecture
The old master builders made use of those ratios which are related to each other by consonant intervals because these are beneficial for our spirit. Above all, these were the triad 1 – c, 3 – g’, 5 – c’’ and its multiples. Study of harmonics is a building block of a new, post-materialist science of life. We are not separated from the cosmos: in the external world of nature we encounter the very forms we carry within us.

There is only one Being.

The language of music is universal. Nature cannot lie. She communicates directly via the aura, i.e. by means of ethereal vibrations, shapes and tones. Music – sound – is the spirit common to all Creation. It acts like an information matrix for communication with all our fellow creatures – plants, crystals, animals. Before we make music, the music makes us.

---

Sources:
Rudolf Haase: Measurable Concordance. Outline of an empirical world harmonics. Klett, Stuttgart 1976

Joachim Ernst Berendt: Nada Brahma. The World is Sound. (de) 1983, (en) publ. Inner Traditions, 1991.

---

Fig. 1 ←Back
Basics for everyone who wants to know the details.
If I take a monochord with a fundamental pitch of C = 138 Hz and divide its string exactly in two, then I produce a pitch which is one octave higher, c. This pitch vibrates twice as quickly, i.e. it has a doubled frequency, 2x138Hz.

If I take one third of the string, the pitch is g with a frequency 3×138 Hz. At one quarter (one half of the half), we have a c again, this time c’, with a frequency of 4×138 Hz.

Fig. 1-2

What we call the harmonic series can be found in many places in nature, for example, if we sound a valveless horn or listen for the chime tones of a guitar string. They can even be heard in the sounds produced by the ‘howling tube’ that our children whirl above their heads.

The harmonic series leads to the following interval ratios:

Konsonanz
Oktave	1	:	2
Quinte	2	:	3
Quarte	3	:	4
Große Sexte	3	:	5
Große Terz	4	:	5
Kleine Terz	5	:	6
Kleine Sexte	5	:	8

Dissonanz
Kleine Septime	5	:	9
Große Sekunde	8	:	9
Große Septime	8	:	15
Kleine Sekunde	15	:	16
Tritonus	32	:	45

It can thus be seen that between the first and second tones of the harmonic series there is an octave = (1:2), between the fifth and eight tone a minor sixth = (5:8) etc.

 

Which makes a fundamental rule very visible:
The lower the number ratios, the stronger the consonance, i.e. the better the harmony. The dashed line more or less represents the place where consonant tones give way to dissonant ones.

Fig. 2  ← Back

ZumPlease click to enlarge the picture.

Fig. 3

 

← Back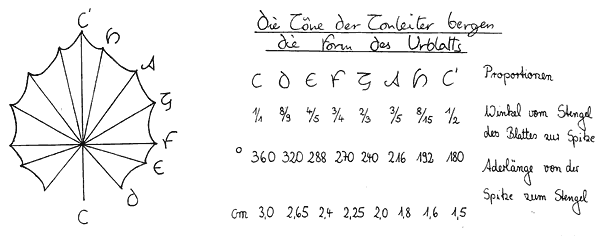Footnote 1
The simplest case of a right-angled triangle that fulfils the theorem is a classic example of harmonics. It concerns a triangle with side lengths of 3, 4 and 5. The sums of the squares of the catheti (9 and 16) is the same as the square of the hypotenuse (25). On the harmonic series, the tones 3, 4 and 5 give the major triad; strings with lengths in a ratio of 3 : 4 : 5 form the minor triad. ← Back

Footnote 2
In many cultures, the number 5 is a symbol of love, eros and sexuality. For example: the 5th day of the week is dedicated to Venus or Freya (veneris dies, vendredi, Friday, Freitag); Hellenistic temples to the goddess of love often had a five-sided floor plan; and in astrology the topic “love” is assigned to the 5th house. ← Back